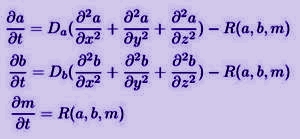The first theory of periodic precipitation was published in 1897 by Wilhelm Ostwald in his book about general chemistry. It is well known, that in some situations, nucleation of crystals can be kinetically hindered, and precipitation can start only at a certain level of supersaturation. This experimental finding formed the basis of Ostwald's "supersaturation theory".

According to this scenario the system remains supersaturated until the formation of the first crystal. At this point a local "explosion" happens because the surrounding zone is very far from equilibrium. "Explosion" means that the chemical reaction becomes so fast, that diffusion is not able to feed it and a wide depleted zone will be formed around the precipitate. This series of events happens repeatedly and causes a spatiotemporal periodicity.

Pros and Cons

With its early come up in some respect the supersaturation model was the most succesfull trial to describe Liesegang patterning. It is capable to explaine the spacing and time law of normal patterns (although it has been mathematically proven only in 1952).

At the same time it is provenly incapable to account for revert patterning or any other anomalies. Following from its mathematical structure it results in infinitely sharp precipitate zones which is not realistic.

The main feature of the sol coagulation theory is that the material to be precipitated is produced first as a colloid dispersion. The visible precipitate will emerge when the stability of this dispersion ceases because of the high concentration of the outer electrolyte.

Pros and Cons

The main problem with this model is the formation of clear spaces, or low density regions. According to the theory the concentration of sol particles decreases in the vicinity of coagulated bands, because they can move by diffusion. Unfortunatelly there is not any experimental evidence for this statement. The mass of sol particles is much greater than that of ions, so their motion must be much slower, supposed that they can move at all in a gel matrix. With such a slow motion they are unable to form wide clear spaces. At the same time in real experiments one can sometimes find 30-40 cm wide empty regions between the 1-2 cm wide bands. It seems to be absolutelly impossible, that the heavy sol particles can travel by random motion to such great distances.

To surmount the mentioned theoretical problem with the sol-coagulation model, many authors tried to describe Liesegang patterning by models, in which the diffusing ions form molecules or very small particles at first. These particles can move by diffusion with practically the same velocity as ions, and when their concentration reaches a treshold, they precipitate. The basic difference between these models lies in the kinetics of precipitation.

Pros and Cons

These models were partially succesfull which means that they result in quasiperiodic patterns that fulfill the spacing and the time law of the Liesegang phenomenon. Even the Matalon-Packter law can be derived on the basis of such mechanisms. At the same time, it seems to be impossible to describe any morphological anomalies in this way.

There are some experimental findings showing that precipitate patterns can form without imposed external concentration gradients. In a gelatine gel containing evenly distributed lead-iodide sol spontaneous pattern formation takes place by a ripening mechanism.

According to the competitive particle growth theory this is due to a thermodinamical instability (Lifshitz-Slyozov instability), that is caused by the nonhomogeneous size distribution of sol particles. Smaller particles have greater surface tension, which causes their solubility to be something higher, than that of the greater ones. This means, that in such a nonhomogeneous system the large particles can grow at the expense of smaller ones. The latters finaly completely dissolve and leave clear regions between the precipitate zones.

Pros and Cons

Polezhaev and Müller have applied succesfully the combination of this and the supersaturation model for the formation of regular Liesegang patterns. Nevertheless in their model they had to suppose the existence of the formerly mentioned diffusive intermedier, and distinguished only two particle sizes ("small" and "large"). This is no doubt the most successfull model of periodic precipitataion since its discovery. According to numerical simulations it performs well both in one and two dimensions, and the authors were able to explain even some morphological anomalies.

Later Krug et al. has developed further the model. In his simulations he has used a complete size distribution function, and a modified, nonlinear growth kinetics.

Basis of every really functioning Liesegang model is the assumption of at least one autocatalytic reaction step in the mechanism of precipitation. In this respect diffusion wave theory is rather exceptional, because it is based on autoinhibition. When two electrolytes react with each other formation of precipitate is always followed by formation of a by-product. There are many cases too, when the reaction can be reversed by excess of this material. For example if the two reactants are MgCl₂ and NH₄OH the by-product will be NH₄Cl, in excess of which the Mg(OH)₂ precipitate can be re-dissolved.

According to the diffusion wave theory spatiotemporal periodicity of Liesegang patterns is caused by the by-product of precipitation. Where a greater amount of precipitate forms concentration of the by-product increases too. This locally increases the solubility product and hinders formation of more precipitate. This inhibition effect remains until the concentration peak is bleared by slow diffusion.

Pros and Cons

From experimental point of view the main problem with this model is that Liesegang patterns can be formed by reactions the by-product of that is water or a completely inert material. Probably this was the cause why diffusion wave theory has never been used in any mathematically exact work, and remained a qualitative model forever.

Adsorption theory gives a very straightforward but - from practical point of view - hardly believable explanation for spatiotemporal periodicity of Liesegang patterns. According to this model appearance of void depleted spaces is caused by adsorption of electrolytes on surfaces of precipitate particles.

Pros and Cons

While such electrolyte adsorption is an existing effect in case of Liesegang patterns it should be very excessive as in some patterns length of void spaces can be half meter!

This model has been suggested recently by Zoltán Rácz and can be regarded as a special variant of the diffusing intermedier models.

According to this description the two electrolytes form a metastable product that can move in the system by diffusion. When its stability ceases it decomposes into immobile precipitate.

Pros and Cons

The spinodal decomposition model has been tested by computer simulation on hypothetical ensembles of spins without any chemical considerations. Although it successfully reproduced the laws of normal patterning, in its entirety it has only rather weak links to real experiments.

Apart from normal patterning there was not any achievement of this approach.

This is essentially a cellular automata model of Liesegang patterning developed recently by Chopard and others. Both reactants are treated as an ensamble of discrete particles walking randomly on a lattice. When two different particles occupy the same lattice position they can react with eachother according to certain automata rules and form an immobile phase (precipitate).

Pros and Cons

This is the first model that addressed the problem of random effects. It was proven to be applicable in 1 and 2 dimensions, successfully reproduced normal patterning, and in one case a propagating defect in a 2D radial arrangement. (It is a little bit misleading that the authors themselves stated that it was a spiral, but on the figure they have published one can see only a crack-like defect.)

Due to the fact that they have tried to describe the recation-diffusion processes on the level of single particles, their method was computationally very intensive.

Later their method has been developed further by Antall et al. using the formerly mentioned spinodal decomposition model. With this modification the mechanism ceased two reproduce any pattern in two dimensions, but successfully reproduced regular Liesegang patterning in one and three dimensions in linear arrangements. They have never been able to reproduce spirals, revert patterning or any other morphological anomalies.