Supersaturation as the common ground

As the starting point of the development of a new comprehensive model of Liesegang patterning I have chosen Ostwalds supersaturation theory. I have done so because bulk simulations have shown that this model - although rather old and oversimplified - can explain almost all of the basic laws.

Ostwald has suggested this model in 1897 and based it purely on a well known effect. He has known that solutions of many substances can be supersaturated, and this metastable state ceases abruptly if a small crystalline material is brought into contact with the solution. This method is called "seeding" and is often applied even nowadays as a preparative technique if the crystallization of a reaction product is kinetically hindered.

According to Ostwalds theory periodic precipitation is nothing more just a "recurrent self-seeding". Although this explanation seems to be absolutely logical for the first sight it has several problems. For example if we try to simulate Liesegang patterns according to this model after a little experimentation we has to realize that in almost all of the cases it produces infinitely sharp precipitate zones whereas in real patterns .

Despite this and other difficulties essentially Ostwalds supersaturation theory formed the basis of the IDNB model.

Bulk simulations

In order to check the overall validity of the IDNB model two series of large-scale simualtions have been performed.

In the first project the original form of the supersaturation model has been examined in about 40.000 different points of the parameter space. In the second a simplified form of the IDNB model has been investigated in the same way.

Although evaluaton of one or several 1D Liesegang patterns is not complicated, doing the same with several thousand such patterns is not necessarily trivial. Therefore a moderately tricky automatic mechanism with an "artificial intelligence" has been developed. This program contained a "pattern detector" that was capable to indicate the existence of a Liesegang pattern with high accuracy in any point of the parameter space.

Armed with such a magic weapon one can perform a computationally efficient scan of a properly chosen hyperbody. Moreover due to the fact that computation of the non-neighbouring points is mathematically independent the whole process can be easily parallelized on a cluster. (In one of my papers I have written down the exact method but in the opinion of the referee the description was "tedious". So here I do not want to bore anybody with the dirty details.)

Results

While value of the spacing coefficient rarely exceeds 1.5 in real experiments, from a purely mathematical point of view the supersaturation model can result in patterns with very high such values. The most probable cause of this apparent disagreement is that simulation is not bounded by certain experimental problems. For example in a simulation we can choose freely the level of supersaturation or the diffusion constants whereas in real experiments there is practically no way to affect these parameters. Another probable cause is the oversimlified nature of the model. This latter is even more probable taking into account that the results of the IDNB model did not show such a controversy.

Data were fitted by orthogonal polynomials. In case of Ostwalds model only the patterns with spacing coefficient lower than 1.5 were used in order to get a realistic picture at first .

Essentially all scaling laws were found to be valid for the whole range of parameters where evaluable patterns detected. (In case of Ostwalds model the width law was certainly not verifiable.) Moreover these vectors form a continuous body in the multidimensional parameter space without holes or disjoint islands.

There were two interesting findings in case of the Matalon-Packter law, and the stronger form of the width law. The former was found to be essentially valid, but the fitted polynomials show that this fenomenological finding is only a very good approximation, but not a generic mathematical property of the studied reaction-diffusion equations.

On the width law

The weaker form of the width law has been found to be valid everywhere in the parameter space.

The stronger form of it simply speaking states that there is an exact mathematical connection between the spacing coefficient and the quotient of the series of zone thicknesses.

Results of bulk simulations at the same time show that although there is indeed a very strong internal similarity between these two scaling laws, they do not have any direct mathematical connection.

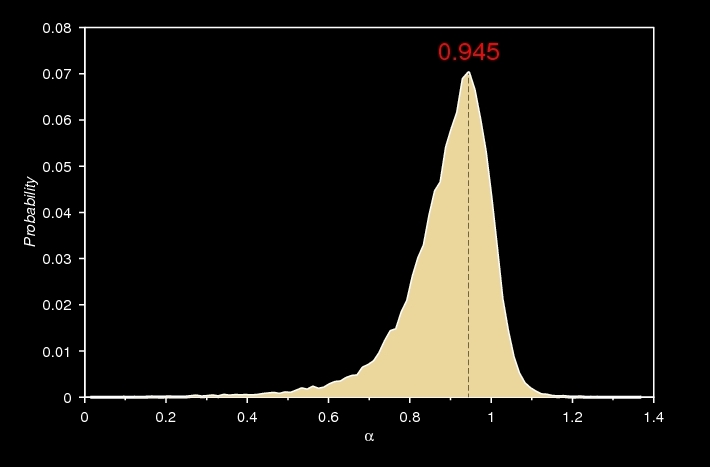
Dependence of zone thicknesses on their positions cannot be described by a simple power law as it was suggested earlier by many workers, because the exponent was not found to be a universal quantity. At the same time its frequency distribution has a rather narrow peak around unity, which elucidates why was it found to be very close to 1.0 in the overwhelming majority of the real experiments.