The "double banding" effect
Double banding is the phenomenon when one Liesegang systems shows two kinds of periodicity. Such patterns look like two different Liesegang systems interleaved. Probably this is the main cause why most of the scientists attributed this anomaly to the presence of pattern forming inpurities.
Although as R. F. Sultan several years ago has shown in his experiments with two salts such a combination of Liesegang systems is indeed possible, here I would like to demonstrate that the same effect can achieved with only one precipitating material.
Simulations with the IDNB model show that there are roughly three variants of double banding. There are bifurcating patterns, classical double banding, and chaotic or completely random strctures. The crossover between them is continuous, while the points in the parameter space that result in a given type of structure seem to form continuous sets.
Bifurcating patterns
When we get close enough to the proper parameter range at first a regularly alternating series of thin and thick bands can be seen. According to the numerical experiences it seems that the cloud of parameter points corresponding to the classical form of double banding is surrounded by a shell of those that result in such bifurcating patterns.
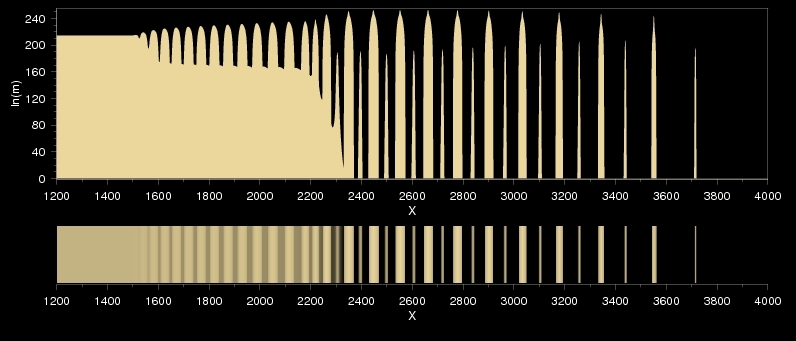
Alternating thin and thick precipitate zones: a special case of the so-called double-banding effect
Classical double banding
Within the proper range we see the double banding effect shown on this figure. This is the classical form, described in the literature: there are sharp, rather densely spaced precipitate zones within the clear regions of a regular Liesegang pattern.
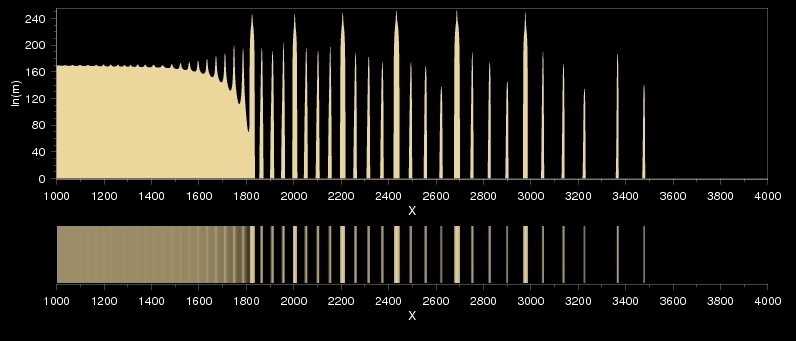
The classical form of double-banding: two different frequencies in the same system with only one precipitating material
Chaotic behaviour
Someweher at the surface between the above described two regions there is a special layer that corresponds to irregular patterns. In these cases there are both promary and secondary zones in the systems, but there is not any apparenmt regularity in their spatial distribution. We can even say, that these are chaotic Liesegang patterns.
It is important to emphasize that there is not any stochastic element in these simulations or in the model. What is shown here is just a mathematically inetersting behaviour of the determinintic form of the unified model of periodic precipitation.
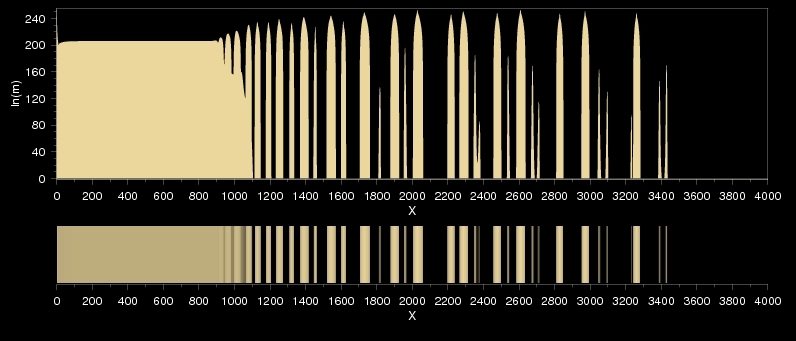
A pattern without any regularity: surprising at first, but this is again only a special case of double-banding