Revert patterns
During the history of Liesegang patterns several experiments resulted in rather weird structures in that the distance between adjacent zones decreased during their development. These systems were like mirror images of normal ones so they are called "revert" patterns.
Enigmatic behaviour
This anomaly has never been addressed by any exact theories, and remained a dark corner of the Liesegang phenomenon.
In a normal Liesegang experiment, positions of the bands can be described by a geometric progression law, and the interspacing between successive zones increases with increasing ordinal number.
A few substances like silver chromate, and ferricianides of nickel, cobalt and copper at the same time have been periodically precipitated in a different manner, where the interspacing of successive rings decreases with their ordinal numbers. This is the so-called revert Liesegang patterning.
According to the literature, revert patterning seems to be a something enigmatic phenomenon. It is rather hard to produce such a pattern intentionally, but sometimes appears abruptly in systems that normally used follow the rules of regular patterning.
Although there were reproducible experiments too, until the IDNB model revert Liesegang patterning lacked of any mathematical or physical explanation.
Three types
Examining the literature one can find that there are three essentially different types of revert patterning mentioned in the different works.
Completely revert patterns
In these cases the whole structure looks like a normal one stood onto its top.
Transitionally revert or mixed patterns
Kanniah et. al. has studied revert Liesegang patterns made of silver-iodide in agar gels. They have paid particular attention to the transition from revert to direct type patterning and have found a certain range of concentrations, where a revert followed by a direct type pattern can be observed in the same system. In such a "mixed" type pattern the distance between successive rings goes on decreasing, reaches a minimum, and then starts to increase with the ordinal number of zones.
Recurrently revert patterns
Probably this is the most weird patterning trend a Liesegang system can produce. The structure consists of many revert type patterns the length of which is increasing along the reaction medium. The whole thing looks like a normal pattern, in which every precipitate zone was replaced by a complete revert Liesegang pattern.
As to my best knowledge this type of anomaly has beeen reported only once since the discovery of Liesegang patterns. At the same time the authors (Kanniah et al.) have found it to be absolutely reproducible, which makes it highly probable that it cannot be simply an experimental failure.
Completely revert patterns
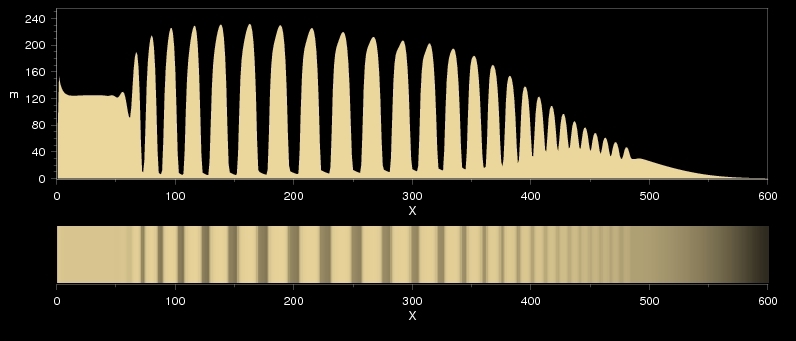
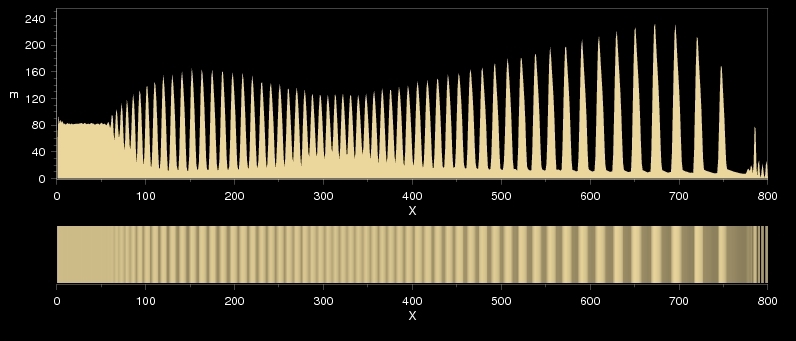
This figure shows a one dimesional revert Liesegang pattern simulated using the IDNB model. The whole habit of the distribution of precipitate is similar to normal patterning. The zones have finite thickness, the distribution is continuous, that is the "void" spaces between the zones are filled with a dilute sol. Even the spacing and time laws remain valid, but now the spacing coefficient is smaller than one.
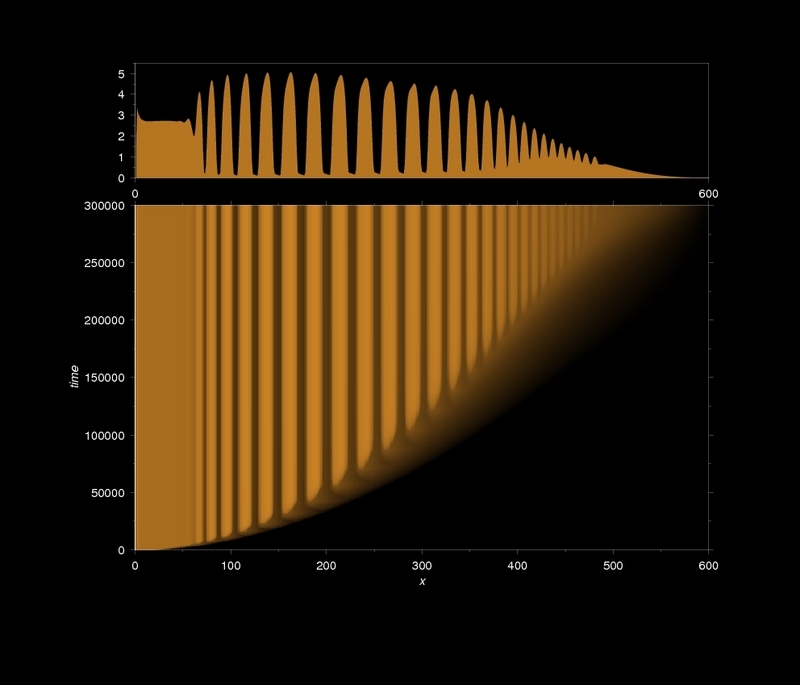
The time law is essentially not affected by revert patterning
Continuous crossover between normal and revert patterning
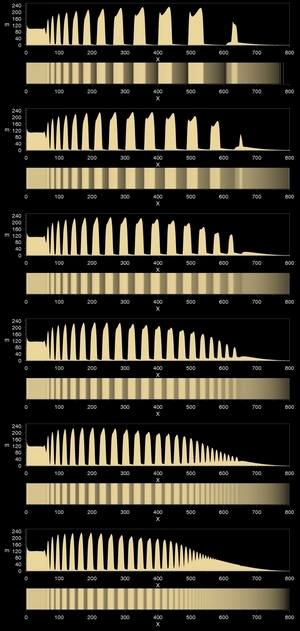
Although revert patterning is rare and hard to reproduce, it is not a completely separate effect as suggested by several authors earlier. As this figure shows there is a continuous crossover from direct to revert patterning.
The cause of uncontrollability
Even the above mentioned enigmatic behaviour of revert patterns can be easily explained on the basis of the IDNB model. Simulations show that some random events that are experimentally usually hardly controllable affect the type of patterning very strongly.
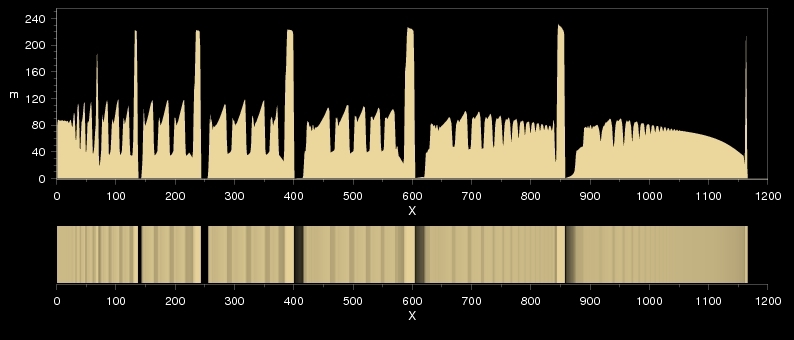
In a laboratory one would think that these four patterns are completely diferent. In reality all parameters were the same in the four simualations and the only difference is a random impact. This is the cause why the real experiments has shown so strong and uncontrollable variability.
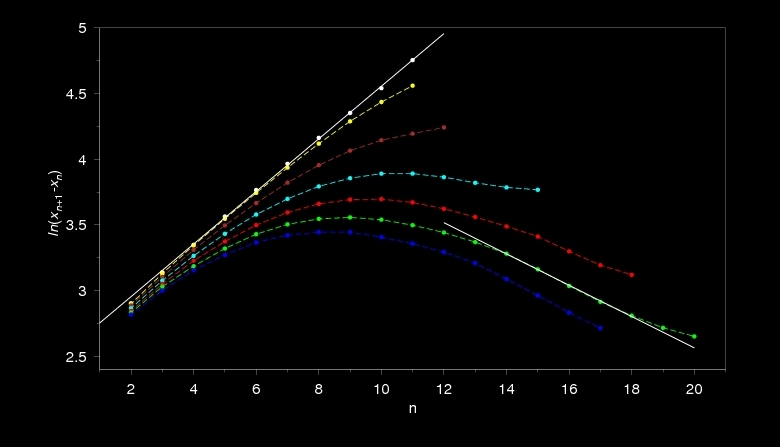
The crossover between normal and revert patterning is continuous
Partially revert structures
Direct and revert patterns can appear in the same system. Kanniah et al. has studied revert Liesegang and payed particular attention to the crossover from revert to direct type patterning. They have found a certain range of concentrations, where a revert followed by a direct type pattern can be observed in the same system. In such a "mixed" type pattern the distance between successive zones goes on decreasing, reaches a minimum, and then starts to increase with the ordinal number again.
The figure shows a representative example for such behaviour reproduced by the IDNB model.
An indirect check of validity
Kanniah et al. have found in their experiments that in case of partially revert structures the positon of the junction point where the normal and revert parts meet shows a definite dependence on the concentration of the outer electrolyte. By increasing the outer concentration the position of this point shifts toward the end of the diffusion column.
As the figure shows the IDNB model can reproduce even this fine detail that seems to be more important if we take into account that this behaviour is something that cannot be "hardwired" into any model. It either will work this way or not, one cannot know it in advance. Therefore succesfull reproduction of such a detail can be regarded as an indirect provement of validity.
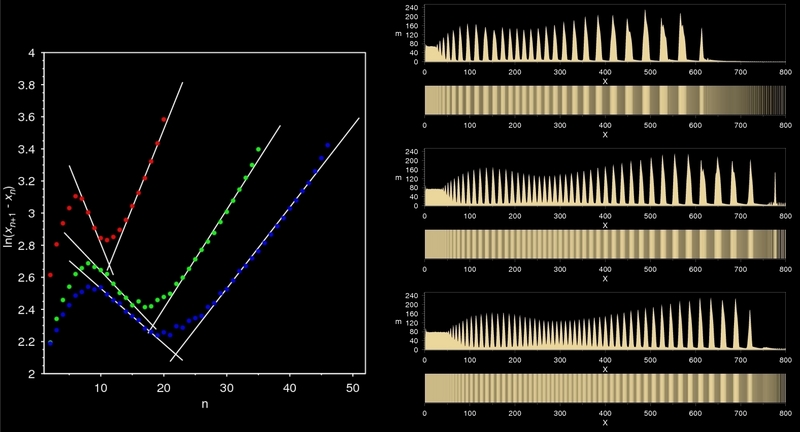
Recurrently revert patterns
Formation of recurrently revert patterns is a "chemical interference" effect. There is another patterning trend, where the zones fall very close to each other and the spacing coefficient is very close to unity. In systems where this effect coincides with revert patterning, the result will be a recurrently revert pattern.
This makes it immediatelly understandable why this patterning mode was observed only once during a century: both above mentioned effects are rather infrequent therefore the probability of their coincidence is almost zero.