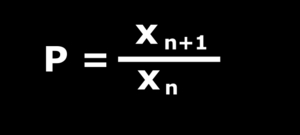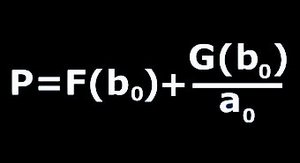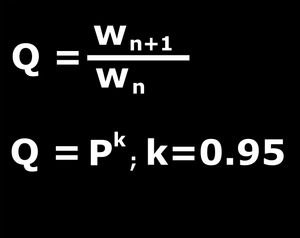Scaling laws of periodic precipitation
Liesegang patterns show several mathematical regularities both in space and time. There are four different scaling laws that govern their formation.

The spacing law
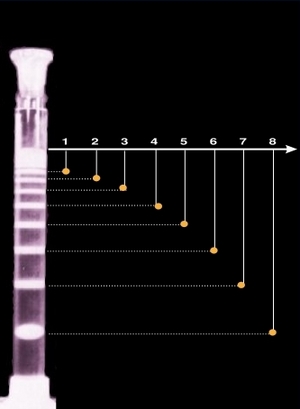
The first such regularity is the so-called spacing law first described by Jablczinsky in 1923. Let us denote by xn the distance of the nth band measured from the gel surface. Jablczinsky has realised that the ratio of the adjacent distances (xn+1/xn) is always constant that is they form a geometrical series. The quotient of this series - that is normally greater than 1 - is often mentioned as the "spacing coefficient" of the structure, and according to many experimental data it is rarely exceeds 1.5.
Although the cause of the spacing law is absolutely not obvious for the first sight, it can be clearly explained on the basis of Ostwald's supersaturation theory. In 1955 Carl Wagner has shown, that if we suppose the existence of precipitate bands, then they have to follow such a geometric progression law.
Normal and revert patterns
There are some examples for anomalous patterns, in which cases the spacing coefficient is smaller than one. These are called "revert patterns" in which the spacing of bands decreases as n increases. In other way the whole structure closely resembles a normal pattern that has been mirrored to its bottom.
The greatest theoretical problem with revert patterns was that acconrding to Wagners formerly mentioned theory their existence is mathematically impossible. But they exist...

The time law
If tn is the time elapsed until the formation of the nth band, it is usually observed, that xn2/tn approaches a constant value, as n increases. This simple mathematical statement, that was first described by Morse and Pierce follows directly from the diffusion-controlled nature of the phenomenon. At the same time, it is not obvious, that this relationship must remain valid in case of an autocatalytic reaction, because the speed of such a process is not a monotonous function of the time.
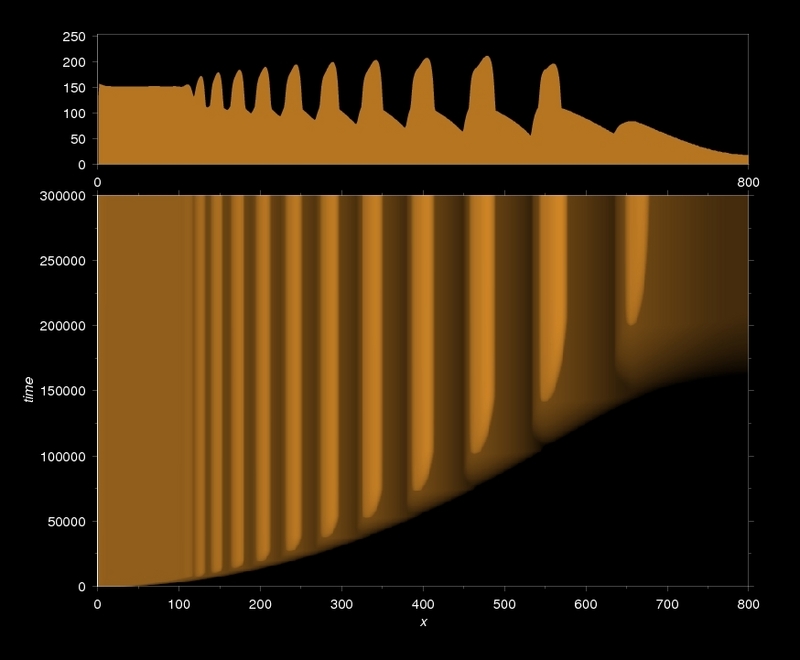
The time law: formation of Liesegang patterns folows a diffusion-controlled kinetics (simulation, IDNB model)

The Matalon-Packter law
Most of the detailed experimental results concern the spacing law. It has been found, that the spacing coefficient is not a universal quantity. It depends both on experimentally controllable and internal parameters. (The latter can be concluded from theoretical considerations, and some experimental ambiguities.)
Dependence of the spacing coefficient on the electrolyte concentrations has been first investigated by Matalon and Packter. They have found in several different experiments that the spacing coefficient (P) is a linear function of 1/a0 where a0 is the concentration of the outer electrolyte (b0). Moreover both the slope and the intersection is a decreasing function of the concentration of the inner electrolyte (b0).

The width law
The width law of Liesegang patterning has a weaker and a stronger form. Using the IDNB model and excessive one dimensional simulations the weaker form has found to be valid, while the stronger can be regarded as a good approximation or as a complete (although elegant) failure depending on ones taste (see below the corresponding menu point).
According to the weaker form of this law if wn denotes the width of the nth precipitate zone then the wn+1/wn ratio is constant, that is the series of zone thicknesses is a geometrical series too.
The stronger form states that if P is the spacing coefficient and Q is the quotient of the width series, then the latter can always be expresed as a power of the former. Several workers have found both in real experiments and theoretical considerations that the exponent of this power is a universal constant and falls between 0.9 and 0.95.