Stochastic resonances

Every process of the world is affected somehow by different random events. The net effect of these usually uncontrollable impacts is called simply "noise". There are many cases when noise is so little that from practical point of view the whole process seems to be completely deterministic and can be described by "mathematically nice" equations. In other cases the presence of the noise is so obvious that the equations can be formulated only through probabilities.

There is however a third class of systems when the noise is practically hidden or seems to be unimportant, but its effect is sometimes observable even on macroscopic level. It means that from experimental point of view such systems can show weird behaviour or put it more simple "miracles" can happen in them.

How to make a miracle - A simple mechanical example

Let us imagine a point-like particle put into a one dimensional symmetrical potential well. Let it have an amount of kinetic energy that is significantly smaller than the depth of the well which means that it is trapped forewer. If there is no friction in the system the particle can oscillate, but never will be able to leave the trap.

Now let us imagine that the oscillating movement of this particle is disturbed by microscopic random events: at random points of time we give a microscopic amoun of extra kinetic energy to it. The impact is random, so the external force will sometimes accelerate the movement, while in other other cases it will a little bit slow down the particle. Because the disturbance itself is microscopic and the time-average of the energy influx is zero, at first sight it seem to be plausible that the deterministic description developed for the ideal noiseless system is still valid.

In many cases this assumption is certainly correct: the movement of the particle will show little glitches but it will never be able to leave the well. And then comes the miracle...

Although the net effect of the noise is zero due to the random nature of the impacts the particle can accumulate the required extra energy and can leave the trap. The probability of this event will be certainly rather low, but not zero.

Such "miraculous" effects that can be traced back to the accumulation of otherwise negligibly small random impacts are called stochastic resonances.

Stochastic effects in radial patterns

Propagating defects

In Liesegang patterns one can often find propagating defect the existence of that is physically paradox. The inconsystency comes from the fact that the development of such a system is diffusion-controlled and diffusion should "iron out" every such glitches.

Simulations show that the appearance of these defects is a stochastic resonance effect. In certain parameter ranges contrary to our expectations the reaction-diffusion mechanism not damps, rather amplifies the effect of microscopic noise.

Returning back to the "particle in the potential well" analogy Liesegang systems seem to have two wells that correspond to two slightly different patterning behaviour. Normally the development of a system takes place exclusively in either the first or in the second. However when the development is disturbed by random noise the virtual particle can jump from one to the other and get stuck there. This is why the defects of Liesegang systems are so stable against the healing impact of diffusion.

Just like in real experiments the above sketched effect exists both in two and three dimensions and does not really depend on the geometry.

Formation of spirals

Formation of spirals is one of the most fascinating anomalies in Liesegang systems. Just like revert patterning this effect cannot be controlled in real experiemnts. Spiral-shaped Liesegang patterns can be produced only by "trial and error" that is indicative of its stochastic nature.

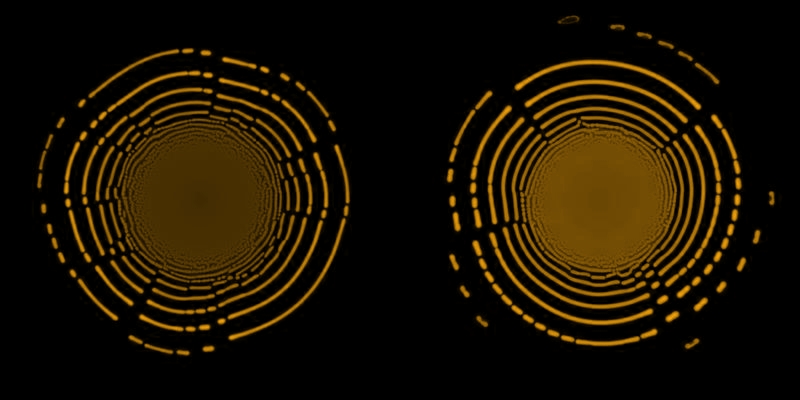
Simulations with the IDNB model validated this - rather straightforward - idea. Depending on the parameters the probability of spiral formation can be greater or lower, but - like the figure below shows - it cannot be told in advance what will be the result is a given simulation. (Development of these two structures can be followed on video too. See the corresponding section.)

Stochastic effects in 3D

The "bouncing ball" effect

In linear Liesegang systems in certain cases the propagating defect can be so wide that it apparently splits the pattern into two halves. These subpatterns however are not independent of each other, because their zones develop alternately. This way the development process of the system looks like a ball that is bouncing between the opposte walls of a narrow channel.

Ball-shaped precipitate zones