Formation of helical Liesegang patterns
One of the most fascinating anomalies in Liesegang patterning is the formation helices and spirals. This can happen both in test tubes (3D helices) and gel sheets (2D spiral), and together with the other formerly mentioned effects has not been entirely explained until now.
Early trials
Until now only one group (Polezhaev et. al.) tried to simulate helices on the basis of their competitive particle growth (postnucleation) model. They have attributed this anomaly basicly to the combination of a wall effect, and an initial asymmetry. The wall is a 2D object, so they have used only a 2D lattice with cylindrical boundary conditions in their simulation. (The real cause was probably that a true 3D simulation was a computationally very intensive task and they did not have the proper computing power.)
Although the final pattern was indeed a spiral (that is not a helix), this result can not be accepted as an explanation of the formation of 3D helices, because this way the authors have completely neglected the diffusion perpendicular to the axis. Test runs performed by the ReaDiVivus system has shown that in a real 3D simulation this latter effect rapidly destroys the helical symmetry.
All in all it is obvious that true 3D simulations cannot be avoided if we want to find the real explanation of helix formation.
Results of the IDNB model
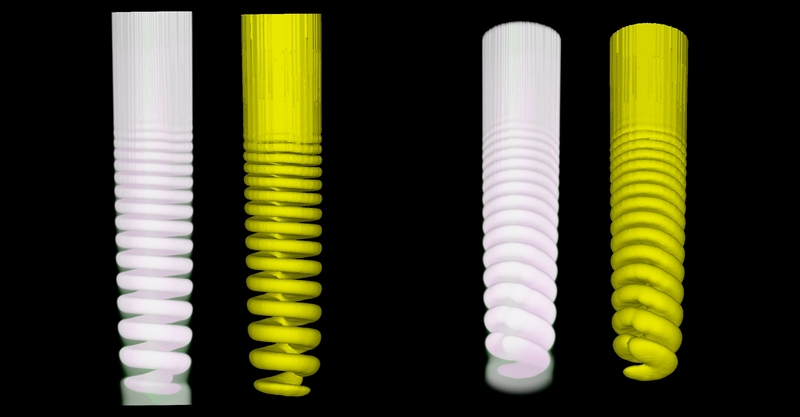
A Liesegang helix from two different viewpoint (volume rendered and isosurface representations). Click on the film icons to see process of evolution.
 |
 |
Knowing the literature it is important to emphasize that - contrary to the common conception - no initial asymmetry in the boundary conditions or any other external impact is needed for the formation of helices. The main cause of their appearance in these systems is a stochastic resonance, that is an effect in which the reaction-diffusion process amplifies the microscopic level random noise.
At the same time there are certain regions of the parameter space where the system becomes more sensible against these random events. In these regions the probability of helix formation is much higher than "normally". For example with the parameters of the pattern shown above this probability is somewhere around 30%, which means that if we perform 10 different simulations on the average only 3 of them will show helical symmetry while the others will be completely normal patterns or only slightly distorted ones.
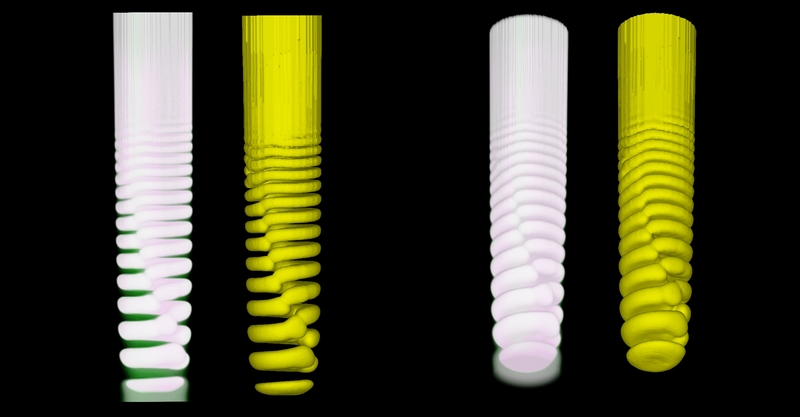
The next figure shows such an "almost-helix".
Although the parameters were the same as above, in this case the effect of random noise was not enough to kick the system into the helical patterning mode
 |
 |
During the simulation of this "almost helical" pattern the same input parameters has been used as above, when the result was a helix. In this case - although from macroscopic point of view the system was completely identical to the former - the random noise was only able to cause a little distortion and it was not enough to kick the system into the helical patterning mode.
In summary formation of helices is a probabilistic process without any deterministic cause or initial asymmetry. Other simulations have even shown that these systems go on their own way during their development and are almost completely insensible against any "tricky" asymmetries introduced artificially.
The essence of the phenomenon is the special interplay between the random and deterministic effects.